Given an integer array of size n and an integer X, we need to determine if there exist two unique elements in the array such that their sum is X. If there are no such elements, we should print There is no such pair.
Approach 1: Finding all unique pairs
This is the brute force approach for the problem. Here, we consider all possible pairs of elements in the array and check their sum. If there is a pair with the sum equal to X, we print that pair and return. If not, we print There is no such pair.
Example:

Time Complexity: O(n2)
Space Complexity: O(1)
Let Us See The Code:
{tab title="C++" class="blue"}
#include <bits/stdc++.h>
using namespace std;
void isPairAvailable(int n,int X,int input_array[])
{
int i,j;
for(i=0;i<n;i++)
{
for(j=i+1;j<n;j++)
{
if(input_array[i]+input_array[j]==X)
{
cout <<"The two numbers are "<< input_array[i]<<" and "<< input_array[j]<< endl;
return;
}
}
}
cout<<"There is no such pair"<<endl;
}
int main()
{
int X=7,input_array[]={1, 5, 3, -2, 4, 7};
int n=sizeof(input_array)/sizeof(input_array[0]);
isPairAvailable(n, X, input_array);//calling the function
return 0;
}
{tab title="Java" class="red"}
/* This code is contributed by Tammisetti Naveen*/
Import java.util.*;
public class PairSum
{
public static void isPairAvailable(int n,int X,int input_array[])
{
//iterating the first element from 0 to n-1
for (int i = 0; i< n; i++)
{
for (int j = i+1; j < n; j++) //iterating the second element from i+1 to n-1
{
if (input_array[i] + input_array[j] == X)//checking the sum of each pair
{
System.out.print("The two numbers are "+input_array[i] +" and "+ input_array[j]);
return;
}
}
}
System.out.print ("There is no such pair");//if there is no pair with given sum
}
public static void main(String arg[])
{
int X = 7, input_array[] = { 1, 5, 3, -2, 4, 7};
int n = input_array.length;
isPairAvailable(n, X, input_array);//calling the function
}
}
{tab title="Python" class="green"}
''' This code is contributed by Arun Reddy'''
def isPairAvailable(input_array, X):
n=len(input_array)
for i in range(n):
for j in range(i+1,n):
if input_array[i]+input_array[j]==X:
print("The two numbers are "+str(input_array[i])+" and "+str(input_array[j]))
return
print("There is no such pair")
if __name__=="__main__":
X = 7
input_array = [1, 5, 3, -2, 4, 7]
input_array.sort()
isPairAvailable(input_array,X)
{/tabs}
Output:
The two numbers are 3 and 4
Approach 2: Two Pointer Approach
In this approach, we first sort the given array. We then use two pointers (say left and right) which are initially pointed to the leftmost and rightmost array elements.
Then we follow the below steps until left is less than right:
If the sum of the elements pointed by these two pointers is equal to X, we print the two elements and stop.
If the sum is less than X, we increment the left pointer by 1.
If the sum is greater than X, we decrement the right pointer by 1.
After accessing all the array elements, if there is no pair with the given sum, we print There is no such pair.
Example:

Time Complexity: O(nlogn)
Space Complexity: O(1)
Let Us See The Code:
{tab title="C++" class="blue"}
/* This code is contributed by Tangudu Sai Kiran */
#include <bits/stdc++.h>
using namespace std;
void isPairAvailable(int n,int X,int input_array[])
{
//finding the pair with given sum using two pointer approach
int left=0,right=n-1;
while(left<right)
{
if(input_array[left]+input_array[right]==X)
{
cout <<"The two numbers are "<< input_array[left]<<" and "<< input_array[right]<< endl;
return;
}
else if(input_array[left]+input_array[right]>X)
right--; //decrement right
else
left++; //increment left
}
cout<<"There is no such pair"<<endl;
}
int main()
{
int X=7,input_array[]={1, 5, 3, -2, 4, 7};
int n=sizeof(input_array)/sizeof(input_array[0]);
sort(input_array,input_array+n); //sorting the array in ascending order
isPairAvailable(n,X,input_array); //calling the function
return 0;
}
{tab title="Java" class="red"}
/* This code is contributed by Tammisetti Naveen*/
import java.util.Arrays;
public class PairSum {
public static void isPairAvailable(int n,int X,int input_array[])
{
int left = 0,right = n-1;
Arrays.sort(input_array);//sorting the array in ascending order
while (left < right)
{
if (input_array[left] + input_array[right] == X)
{
System.out.print("The two numbers are "+input_array[left] +" and "+ input_array[right]);
return;
}
else if (input_array[left] + input_array[right] > X)
right--; //decrementing the right index
else if (input_array[left] + input_array[right] < X)
left++; //incrementing the left index
}
System.out.print("There is no such pair");
}
public static void main(String arg[])
{
int X = 7, input_array[]= {1, 5, 3, -2, 4, 7};
int n = input_array.length;
isPairAvailable(n, X, input_array);//calling the function
}
}
{tab title="Python" class="green"}
''' This code is contributed by Arun Reddy '''
def isPairAvailable(input_array, X):
left,right=0,len(input_array)-1
while left<right:
if(input_array[left]+input_array[right]==X):
print("The two numbers are "+str(input_array[left])+" and "+str(input_array[right]))
return
elif(input_array[left]+input_array[right]<X):
left+=1
else:
right-=1
print("There is no such pair")
if __name__=="__main__":
X = 7
input_array = [1, 5, 3, -2, 4, 7]
input_array.sort()
isPairAvailable(input_array,X) {/tabs}
Output:
The two numbers are 3 and 4
Approach 3: Using Hashing
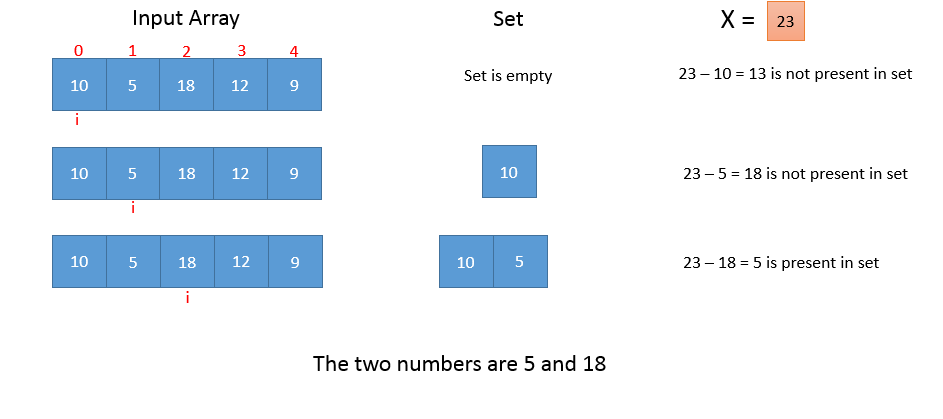
In this technique, we linearly access each element in the array. Let us say input_array[i] is an array element at a given instance. We check if X - input_array[i] has been previously accessed from the array. For this, we use a data structure which takes time complexity : O(1) to find an element.
If X - input_array[i] is previously accessed from the array, we print that pair and return.
If not, we go to the next element in the array.
After accessing all the array elements, if there is no pair with the given sum, we print There is no such pair.
Example:
Time Complexity: O(n)
Space Complexity: O(n)
Let Us See The Code:
{tab title="C++" class="blue"}
/* This code is contributed by Tangudu Sai Kiran */
#include <bits/stdc++.h>
using namespace std;
void isPairAvailable(int n,int X,int input_array[])
{
unordered_set<int> Set; //creating unordered set
//fast retrieval of individual elements based on their value
int difference;
for(int i=0;i<n;i++)
{
difference = X - input_array[i];
if(Set.find(difference) != Set.end()) //searching for difference in unordered set
{
cout <<"The two numbers are "<< difference <<" and "<< input_array[i]<< endl;
return;
}
Set.insert(input_array[i]); //inserting input_array[i] if difference is not present in set
}
cout<<"There is no such pair"<<endl;
}
int main()
{
int X=7,input_array[]={1, 5, 3, -2, 4, 7};
int n=sizeof(input_array)/sizeof(input_array[0]);
isPairAvailable(n, X, input_array);//calling the function
return 0;
}
{tab title="Java" class="red"}
/* This code is contributed by Tammisetti Naveen*/
import java.util.HashSet;
import java.io.*;
public class PairWithGivenSum
{
public static void isPairSum(int n,int X,int input_array[])
{
HashSet Set = new HashSet ();//Creating an hashset
for (int i = 0;i < n; i++)
{
int difference = X - input_array[i];
if (Set.contains(difference))//Checking whether the hashset contains the difference of sum and a
{
System.out.print("The two numbers are "+ difference +" and "+ input_array[i]);
return;
}
Set.add(input_array[i]);//adding the values in array in hashset
}
System.out.print("There is no such pair");
}
public static void main(String args[])
{
int X = 7, input_array[]= {1, 5, 3, -2, 4, 7};
int n = input_array.length;
isPairSum (n, X, input_array);//calling the function
}
}
{tab title="Python" class="green"}
''' This code is contributed by Arun Reddy'''
def isPairAvailable(input_array,X):
Set=set()
for i in input_array:
if X-i in Set:
print("The two numbers are ",(X-i)," and ",i)
return
Set.add(i)
print("There is no such pair")
if __name__=="__main__":
X = 7
input_array = [1, 5, 3, -2, 4, 7]
input_array.sort()
isPairAvailable(input_array,X)
{/tabs}
Output:
The two numbers are 3 and 4
Contributors for this Article: Tangudu Sai Kiran, Tammisetti Naveen, Arun Reddy