Given a string consisting of 0's and 1's, we need to find the equivalent decimal number of the binary string.
Approach:
The approach we use here is similar to that we use while calculating the decimal number using pen and paper.
EXAMPLE:
Let "1010" be the given string.
Equivalent binary number is (1*23)+(0*22)+(1*21)+(0*20) = 8+0+2+0 = 10
From the above example we can observe two points :
- When the element of string is
'0', there is no need of performing any operation. This is because 0 multiplied by any number gives 0. - When the element of the string is
'1', we can simply add thepth power of 2. This is because 1 multiplied by any number gives the number itself.
So, we can conclude that it is simply sufficient to add the pth power of 2 whenever we find '1' in the string.
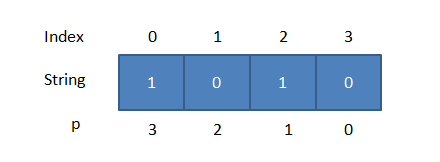
How do we get the value of p ?
Remember that p is always 0 for the LSB (Least Significant Bit) i.e. last character of the string. As we approach towards the MSB (Most Significant Bit), the value of p is incremented by 1 unit.
The time complexity of this approach is O(N) where, N is the length of binary string.
LET US SEE THE CODE:
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;
cout << "Enter the binary string" << endl;
cin >> s; // Taking binary string as input
int i,N,decimal_number=0,p=0;
N=s.size(); // storing the size of string in N
for(i=N-1;i>=0;i--) // starting the loop from LSB
{
if(s[i]=='1') // Checking if string element is 1
{
decimal_number+=pow(2,p); // if yes, adding the pth power of 2 to the decimal_number
}
p++; // incrementing the value of p as we move towards MSB
}
cout << "Equivalent decimal number is " << decimal_number << endl;
}
TESTCASE:
Enter the binary string 1100 Equivalent decimal number is 12