Brute force Approach to find GCD of Two numbers:
In this approach we first check if both a and b have the value 0. If yes, the GCD(a,b) is not defined.
If not we check if either of a and b is 0. In this case the non-zero number among a and b is the GCD(a,b).
If the values of both a and b is not 0, we check for all numbers from 1 to min(a,b) and find the largest number which divides both a and b. This largest number which divides both a and b is said to be the GCD(a,b).
EXAMPLE:
let a=5 b=10
min(a,b)=min(5,10)=5
numbers between 1 to 5 are 1,2,3,4,5
The highest number which divides both 5 and 10 is 5
So, GCD(5,10)=5
Time Complexity : O(min(a,b))
Space Complexity : O(1)
C++ Program for Brute force GCD:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int a,b,mi,gcd,i;
cout << "Enter the values of a and b" << endl;
cin >> a >> b; // Taking a and b as input
if(a==0 && b==0) // checking if the values of both a and b are 0
{
cout << "GCD is not defined" << endl;
}
else if(a==0) // checking if the value of a is 0
{
cout << "GCD of " << a << " and " << b << " is " << b << endl;
}
else if(b==0) // checking if the value of b is 0
{
cout << "GCD of " << a << " and " << b << " is " << a << endl;
}
else
{
mi=min(a,b); // finding the min of a and b
for(i=1;i<=mi;i++) // loop to check numbers from 1 to mi(a,b)
{
if(a%i==0 && b%i==0) //checking if i is divisible by both a and b
{
gcd=i; // if yes, updating the value of gcd with i
}
}
cout << "GCD of " << a << " and " << b << " is " << gcd << endl;
}
return 0;
}
TESTCASE:
Enter the values of a and b
37 55
GCD of 37 and 55 is 1
Euclidean Algorithm to find GCD of Two numbers:
If we recall the process we used in our childhood to find out the GCD of two numbers, it is something like this:
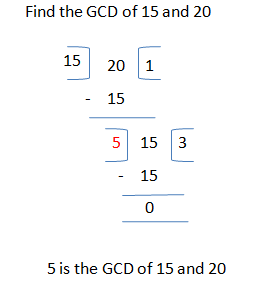
This process is known as Euclidean algorithm.
The idea behind this algorithm is,
GCD(a,b) = GCD(b,r0) where, a = bq0 + r0 and a>b
GCD(b,r0) = GCD(r0,r1) where, b = r0q1 + r1 and b>r0
GCD(r0,r1) = GCD(r1,r2) where, r0= r1q2 + r2 and r0>r1
.
.
GCD(ri-1,ri) = GCD(ri,0) where, ri-1 = riqi+1 + 0 and ri-1>ri
GCD(ri,0) = ri (Since, GCD(k,0) = k and k != 0)
Why is GCD(a,b) = GCD(b,r0) ?
Let g = GCD(b,r0)
r0 = g*c1
b = g*c2
a = bq0+r0
a = (g*c2)q0 + (g*c1)
a = g * (c2q0 + c1)
So we can say that g is also the GCD(a,b) (Since, c1=1 or c2 and c1 do not have any common factors)
therefore, GCD(a,b) = GCD(b,r0)
EXAMPLE:
Let a=32 b=10
GCD(32,10) = GCD(10,5) [32=10(3)+2]
GCD(10,5) = GCD(2,0) [10=2(5)+0]
GCD(2,0) = 2
So, GCD(32,10) = 2
Time Complexity : O(log(min(a,b)))
Space Complexity : O(1)
C++ program for GCD using Euclidean Algorithm:
#include<bits/stdc++.h>
using namespace std;
int find_gcd(int a,int b);
int main()
{
int a,b,gcd;
cout << "Enter the values of a and b" << endl;
cin >> a >> b; // Taking a and b as input
if(a==0 && b==0) // checking if the values of both a and b are 0
{
cout << "GCD is not defined" << endl;
}
else
{
gcd=find_gcd(a,b); // calling the function to find gcd of a and b
cout << "GCD of " << a << " and " << b << " is " << gcd << endl;
}
return 0;
}
int find_gcd(int a,int b) // reccursive function to find gcd of a and b
{
if(a==0) // cheching if value of a is 0
return b; // if yes, returning the value b
else if(b==0) // cheching if value of b is 0
return a; // if yes, returning the value a
else if(a==b) // checking if the value of a and b is equal
{
return a; // if yes, returning gcd=a=b
}
else
{
if(a>b) // checking if a is greater than b
{
return find_gcd(b,a%b); // if yes, returning the gcd of b and reminder of a when divided by b
}
else
{
return find_gcd(a,b%a); // if no, returning the gcd of a and reminder of b when divided by a
}
}
}
TESTCASE:
Enter the values of a and b
56 24
GCD of 56 and 24 is 8