Given an integer N, we need to find all the prime numbers between 1 to N (inclusive).
The naive approach for this problem is to perform Primality Test for all the numbers from 1 to N which takes a time complexity of O(N3/2). There is an efficient approach to this problem, known as Sieve Of Eratosthenes.
In this approach, we consider an array say prime_array with indices representing the numbers from 1 to N. The elements of prime_array can have value either 0 or 1. Marking an array element as 0 represents that the index of the array element is prime and marking an array element as 1 represents that the index of the array element is non-prime.
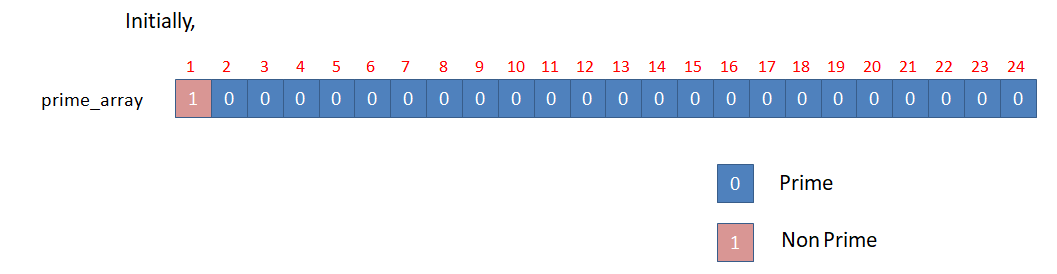
Initially, we consider that all the numbers from 1 to N are prime. So, we initialize the prime_array with 0. But remember that 1 is neither prime nor composite. So we mark prime_number[1] = 1.
Later, we find out all the composite numbers between 1 to N and mark their corresponding prime_array elements as 1.
How do we find the composite numbers between 1 to N ?
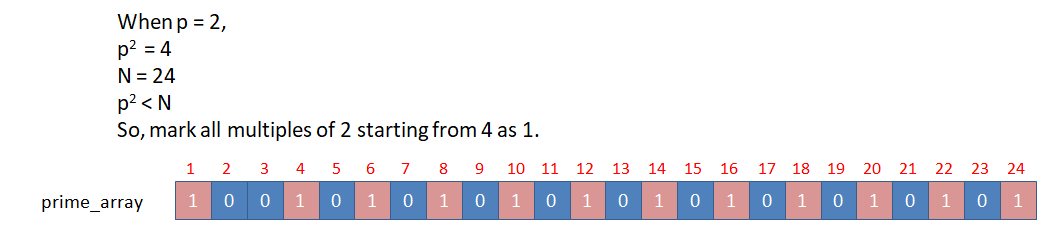
For this, we consider each marked prime number (say p) from 2 to N and mark all its multiples other than p (within N) as composite.
This is because the multiples of a prime number other than the number itself are always composite.
i.e.,
If p = 2 (4,6,8,10,12,14,16,18,20... are marked composite)
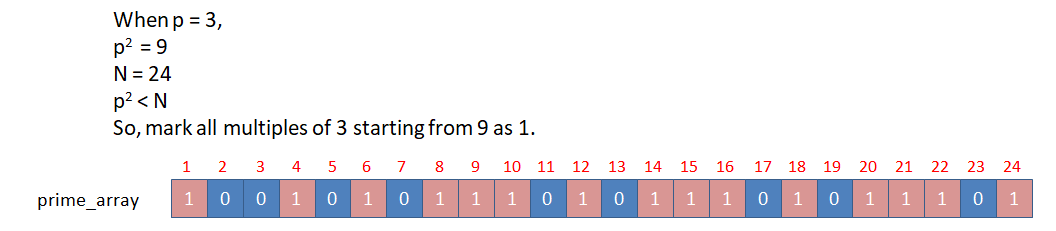
If p = 3 (6,9,12,15,18,21,24,27,30... are marked composite)
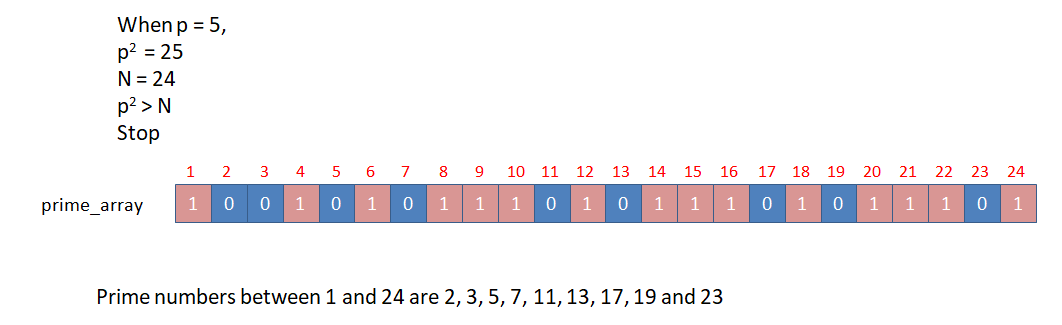
If p = 5 (10,15,20,25,30,35,40,45,50... are marked composite)
.
.
If p = i (i*2,i*3,i*4,i*5... are marked composite)
But as we observe,
For p = 3, 6 is already marked composite by p = 2. So it is not required to mark it composite by p = 3 again.
For p = 5, 10,15,20 are already marked composite by p = 2 and p = 3. So it is not required to mark them composite again.
Therefore, instead of marking all the multiples of p as composite, it is sufficient to mark the multiples greater than p*(p-1).
Note :
It is sufficient to consider p until its value is equal to √N.
This is because,
Once p is greater than the square root of N (p > √N),
p2 exceeds N (p2 > N) and we do not need the prime numbers succeeding N.
After marking the corresponding prime_array elements of all the composite numbers, we can easily differentiate the prime numbers and composite numbers between 1 and N.
SIEVE OF ERATOSTHENES APPROACH WITH AN EXAMPLE:
Let N = 24
Time complexity: O(N*log(log(N)))
Space complexity: O(N)
CODE FOR SIEVE OF ERATOSTHENES:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int N,p,i;
cout << "Enter the value of N" << endl;
cin >> N; // Taking N as input
vector<int> prime_array(N+1,0); // Initialising prime_array to 0
prime_array[0]=1; // marking prime_array[0] to 1 because 0 is neither prime nor composite
prime_array[1]=1; // marking prime_array[1] to 1 because 1 is neither prime nor composite
for(p=2;p<=N;p++) // loop to access all numbers between 1 and N
{
if(p*p>N) // checking if the square of any numbers is greater than N
{
break; // if yes, break the loop
}
if(prime_array[p]==0) // checking if p is marked as prime number
{
for(i=p*p;i<=N;i+=p) // loop to mark the multiples of p with 1
{
prime_array[i]=1;
}
}
}
cout << "Prime numbers between 1 and " << N << " are :"<< endl;
for(i=0;i<=N;i++) // loop to print the prime numbers between 1 to N
{
if(prime_array[i]==0) // checking if ith element of prime_array is 0
{
cout << i << " "; // if yes, print i
}
}
return 0;
}TEST CASE:
Enter the value of N
30
Prime numbers between 1 and 30 are :
2 3 5 7 11 13 17 19 23 29
Same approach can also be used to count the number of prime numbers between 1 and N.