Binary Search Algorithm With Example

Consider that you are given a book and asked to open a page with particular page number. How will you do that?

Will you check each and every page for the page number (Linear Search)?

No, you will simply open a random page and compare its page number with the given page number. If the given page number is less than the page number of the random page, then you will search the previous pages from that random page.

Whereas, if the given page number is greater than the page number of the random page, then you will search the next pages to the random page.
This process continues until the random page has the page number equal to the given page number.

The same idea is used in Binary Search. Binary search is also known as Logarithmic Search or Half-Interval Search. It uses the principle of Divide and Conquer.

In this approach, the input_array is in sorted order. We use three variables low, high and mid to minimize the no.of elements to be searched at every stage.
Here, low is the index of starting element of the sub-array to be searched, high is the index of last element of that sub-array and mid is the index of middle element of that sub-array.

Note : At each stage, the sub-array is reduced to half of its length.

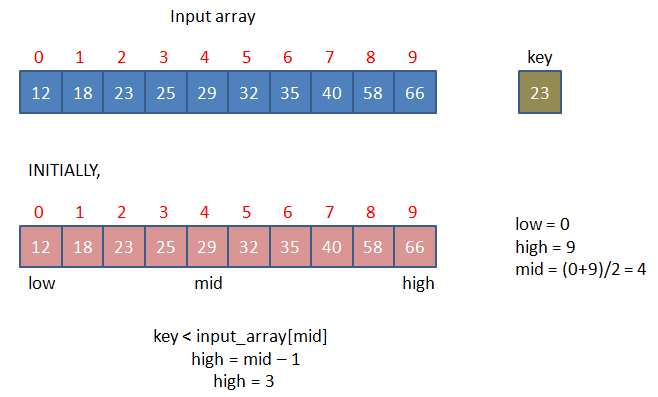
Initially, the complete array is to be searched (sub-array = input_array). So low = 0, high = N - 1 (where, N is the length of input_array ) and mid = (N-1)/2.

At each stage, mid is calculated by the formula, mid = (low+high)/2. After finding the mid value, we compare input_array[mid] with key.

• If key < input_array[mid], we need to search the key in the first half of the sub-array. So, high = mid - 1. Now the sub-array ends at mid - 1.
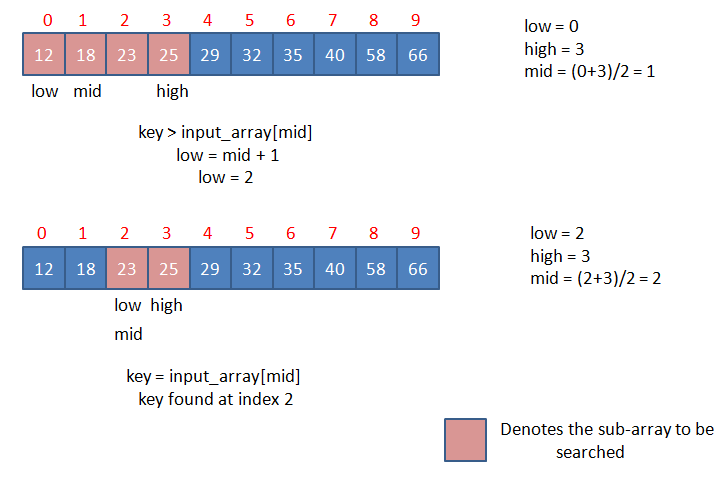
• If key > input_array[mid], we need to search the key in the second half of the sub-array. So, low = mid + 1. Now the sub-array starts from mid + 1.
• If key == input_array[mid], key is found at the position mid of input_array.

Let us look at binary search with an example:

Let input_array = {12, 18, 23, 25, 29, 32, 35, 40, 58, 66} and key = 18

Advantage of binary search:
During each comparison, 50% of the elements are eliminated from the sub-array.
Disadvantage of binary search:
This algorithm does not work if the input_array is not in sorted order.

Time Complexity : O(log₂N)
Space Complexity : O(1)

The binary search algorithm time complexity is better than the Linear search algorithm. The given code written in C++, we can write program for binary search in both recursive and non-recursive approaches.

C++ CODE FOR BINARY SEARCH:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int N,i,low,mid,high,key;
    cout << "Enter the length of array" << endl;
    cin >> N; // Taking length of array as input
    int input_array[N];
    cout << "Enter array elements in increasing order" << endl;
    for(i=0;i<N;i++) // loop to take array elements as input
    {
        cin >> input_array[i];
    }
    cout << "Enter the element to be searched" << endl;
    cin >> key; // taking key as input
    low=0; // initialising low to 0 because initially sub-array is the input_array
    high=N-1; // initialising high to N-1 because initially sub-array is the input_array
    while(low<=high) // the index of first element of sub-array is always less than or equal to the index of last element of sub-array
    {
        mid=(low+high)/2; // finding the index of middle element in sub-array
        if(key<input_array[mid]) // checking if key is less than the middle element of sub-array
        {
            high=mid-1; // if yes, sub-array ends at index mid-1
        }
        else if(key>input_array[mid]) // checking if key is greater than middle element of sub-array
        {
            low=mid+1; // if yes, sub-array starts from mid+1
        }
        else
        {
            // if key is equal to middle element of sub-array, there is no need of searching the remaining elements
            break;
        }
    }
    if(key==input_array[mid]) // if key is equal to middle element of sub-array, mid is the position of key
    {
        cout << "key found at index " << mid << endl;
    }
    else // if not, key is not found in input_array
    {
        cout << "key is not found in the array" << endl;
    }
    return 0;
}

TESTCASE :

Enter the length of array
5
Enter array elements in increasing order
14 35 67 89 90
Enter the element to be searched
67
key found at index 2

you can refer the following C Program to Search an Array Element using BINARY SEARCH, JavaScript Function to perform Binary Search and C Program to find an Element using Binary Search.